[자료구조] 그래프(Graph)
2022년 04월 05일
그래프(Graph)
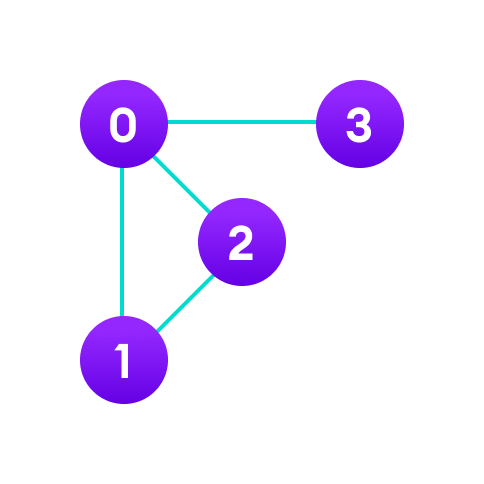
그래프는 정점(Vertex)와 간선(Edge)로 이루어진 자료 구조이다.
일상 생활에서 SNS에서의 사람들 간의 관계, 지하철 노선도, 지도 어플리케이션 등을 예로 들 수 있다.
용어
- -정점(Vertex) : 꼭짓점, 위치, 노드(node)라고도 함
- -간선(Edge) : 정점들을 연결하는 선, 분기(branch)라고도 함
- -인접 정점(Adjacent Vertex) : 어떠한 정점에서 직접 연결된 정점
- -차수(degree) : 정점에 연결된 간선의 수
그래프 구현 방법
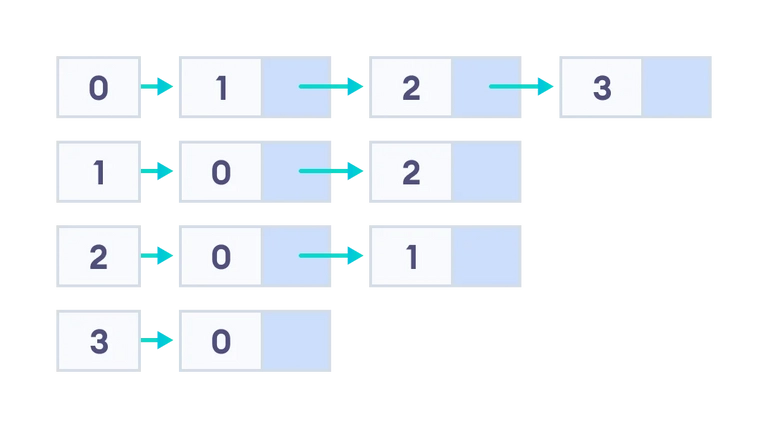
인접 리스트(Adjacency List)
각 정점에 인접한 정점들은 연결 리스트로 연결한 것
즉, 정점의 개수만큼 인접 리스트가 존재하고 각각의 인접 리스트에는 인접한 정점의 정보가 저장된다.
특징
-
-존재하는 간선만 관리하면 되기 때문에 메모리 측면에서 효율적이다.
-
-그래프의 모든 간선의 수를 구하려면 각 정점의 헤더 노드부터 인접 리스트를 탐색해야 하기 때문에 O(n + e)의 시간 복잡도를 갖는다.
-
-두 정점을 연결하는 간선을 조회하거나 정점의 차수를 구하기 위해서는 정점의 인접 리스트를 탐색해야하므로 정점의 차수만큼 O(degree(v))의 시간 복잡도를 갖는다.
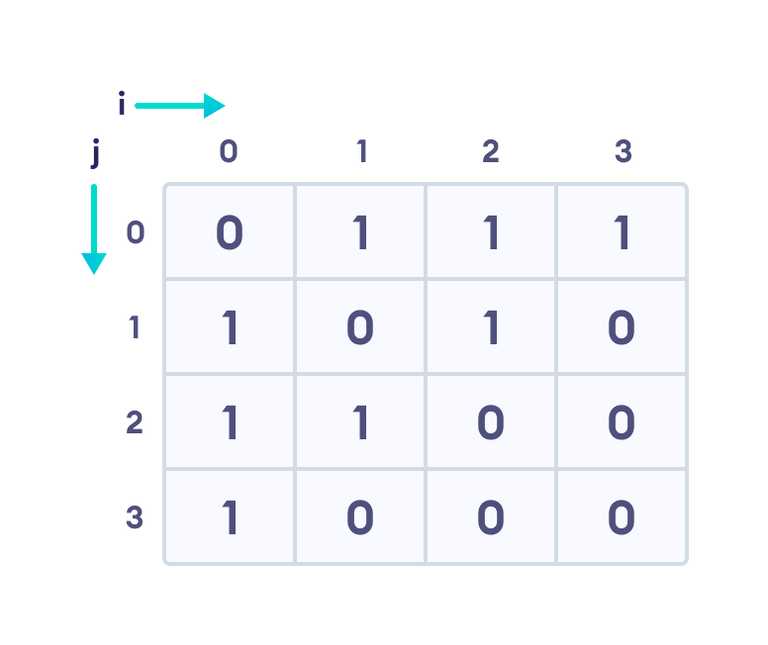
인접 행렬(Adjacency Materix)
그래프의 정점을 2차원 배열로 만든 것
만약 정점의 개수가 n이면, n x n 형태의 2차원 배열이 인접 행렬로 사용된다.
각 행과 열은 정점을 나타내며, 각 원소들은 간선을 나타낸다.
특징
-
-2차원 배열에 모든 정점들의 간선 정보가 들어 있기 때문에, 두 정점을 연결하는 간선을 조회할 때의 시간 복잡도는 O(1)이다.
-
-정점의 차수를 구할 때, 인접 행렬의 행의 값을 모두 더하면 되기 때문에 시간 복잡도는 O(n)이다.
-
-간선의 수와 상관없이 항상 n^2 크기의 2차원 배열이 필요하기 때문에 메모리 낭비가 발생한다.
-
-그래프의 모든 간선의 수를 구하려면 인접 행렬 전체를 확인해야하므로 O(n^2)의 시간 복잡도를 가진다.
연결 리스트로 그래프 구현하기(JS)
class Graph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if (!this.adjacencyList[vertex]) {
this.adjacencyList[vertex] = [];
return true;
}
return false;
}
addEdge(vertex1, vertex2) {
if (this.adjacencyList[vertex1] && this.adjacencyList[vertex2]) {
this.adjacencyList[vertex1].push(vertex2);
this.adjacencyList[vertex2].push(vertex1);
}
}
removeEdge(vertex1, vertex2) {
if (this.adjacencyList[vertex1] && this.adjacencyList[vertex2]) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
(v) => v !== vertex2
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
(v) => v !== vertex1
);
return ture;
}
return false;
}
removeVertex(vertex) {
if (!this.adjacencyList[vertex]) return undefined;
// 연결 고리 다 제거
while (this.adjacencyList[vertex].length) {
let temp = this.adjacencyList[vertex].pop();
this.removeEdge[(vertex, temp)];
}
// 연결 고리 다 제거했으면 vertex 제거
delete this.adjacencyList[vertext];
return this;
}
}Tags